【brainpy学习笔记】神经元的电导模型——以HH模型为例

以经典的Hodgkin-Huxley模型为例，介绍神经元电导模型的brainpy实现。

Fellyhosn

4215人浏览 · 2023-04-11 21:19:01

Fellyhosn · 2023-04-11 21:19:01 发布

参考书目：《神经计算建模实战——基于brainpy》吴思

以经典的Hodgkin-Huxley模型为例，介绍神经元电导模型的brainpy实现。

1.神经元结构与静息膜电位

一些高中生物＆人解知识回顾

神经元是大脑内信息处理的基本单位，由细胞体、树突、轴突构成
两个神经元通过突触连接
神经元有多种形态（单极、双极、多级、假单极等）
当细胞膜内外的离子浓度差产生了一种化学梯度时，离子从高浓度区域流向低浓度区域
电荷梯度是由细胞内外的电位差产生的（例如K+流向细胞外使得胞外带正电、胞内带负电）
化学梯度和电荷梯度作用相反，当化学扩散的动力和电场力相互平衡时，离子净流动量为0，称此时的膜电位为该离子的平衡电位
当细胞膜对多个离子通透时，细胞膜静息时的平衡电位可用GHK方程计算

2.等效电路

与物理电学知识的结合，将离子在胞内外的转移等效为一个电路模型，从而方便对其进行分析。通常情况下，等效电路模型包含三个部分：

电阻器：离子通道
电源：离子浓度梯度
电容器：细胞膜储存电荷能力

建模过程：

考虑简化的模型（只对钾离子通透），记细胞膜电容为 $C_m$ ，钾离子通道由一个等效电阻 $R_K$ 和等效电源 $E_K$ 表示，离子通道的电导 $g_K=1/R_K$ ,细胞膜两端电压差为 $V_M$ ，等效电路模型如图：

电容器储存的电荷量： $q=C_MV_M$
引入单位膜电容 $c_M$ 表示细胞膜单位面积电容量（通常接近于 $1\mu F/cm^2$ ）对上式求导得到流过细胞膜的单位电容电量 $I_{cap}=c_M\frac{dV_M}{dt}$
根据欧姆定律，流过钾离子通道的电流为 $I_K=g_K(V_M-E_K)=\frac{V_M-E_K}{R_K}$
根据基尔霍夫电流定律，进入电池的总电流和为0，因此有： $0=I_{cap}+I_K=c_M\frac{dV_M}{dt}+\frac{V_M-E_K}{R_K} \Rightarrow c_M\frac{dV_M}{dt}=-\frac{V_M-E_K}{R_K}=-g_K(V_M-E_K)$

将模型拓展到更一般的情况（考虑细胞膜同时对钠离子、钾离子、氯离子通透，并接收一个外界输入电流 $I(t)$ ）

此时细胞膜单位面积的离子电流 $i_{ion}=-g_{Cl}(V_M-E_{Cl})-g_K(V_M-E_K)-g_{Na}(V_M-E_{Na})$
神经元总表面积为A，将 $I(t)$ 除以A得到单位膜面积接受到的电流
记单位膜电阻 $r_M=1/(g_{Cl}+g_K+g_{Na})$
记细胞静息膜电位 $E_R=(g_{Cl}E_{Cl}+g_KE_K+g_{Na}E_{Na})r_M$
重写2中式子： $c_M \frac{dV_M}{dt}=-\frac{V_M-E_R}{r_M}+\frac{I(t)}{A}$
得到细胞膜电位的稳定态：

3 电缆方程与动作电位

将神经纤维等效为半径为a的圆柱形电缆，考察在任意位置x处电流变化情况，建立等效模型如图：

紫色式子由基尔霍夫定律得到，最终可推导出电缆方程（绿色式子）

如果电信号在很长的神经纤维中被动传输，则在传输的过程中信号衰减导致无法在生物体内进行长距离传输。而髓鞘充当绝缘层的作用，保护电信号在传播过程中不受到较大的衰减。同时，神经系统在间隔200μm到2mm之间会规律地出现郎飞氏结，动作电位能在一个髓鞘中快速传播至下一个郎飞氏结，由此完成跳跃性传导。

4 HH模型

4.1 背景

HH模型即Hodgkin-Huxley模型，由艾伦·霍奇金（Allen Hodgkin）和安德鲁·赫胥黎（Andrew Huxley）提出，两人在1939年首次合作，但仅几个月后，第二次世界大战爆发，两人在战争期间均转向研究武器。战争结束后，两人继续合作，并于1950年提出HH模型。1963年两人因此共同获得了诺贝尔生理学或医学奖。可见战争对科技的阻碍以及和平的不易！

4.2 离子通道模型

每个离子通道都被视为一个由多个闸门控制的孔，离子从闸门出入，每个闸门只有开和闭两个状态且各个闸门间的状态相互独立。由于模拟单个闸门的打开or关闭太过复杂，于是在宏观上模拟闸门打开/关闭的比例，使用一阶转换概率来建模。

令m为闸门打开的比例，则1-m是闸门关闭的比例， $\alpha(V),\beta(V)$ 分别表示闸门从关闭到打开/打开到关闭的电压依赖的速率，可列出微分方程： $\frac{dm}{dt}=\alpha(V)(1-m)-\beta(V)m$

在HH模型中，参数均可以通过实验数据拟合得到。

4.3 如何测量离子电流与泄露电流：电压钳

Hodgkin和Huxley使用电压钳技术测量总的离子电流 $i_{ion}$ 和泄露电流的电导 $g_L$ 。电压钳允许实验者将膜电位保持在恒定值，此时电容性电流 $I_{cap}=c\frac{dV}{dt}=0$ ，在电压钳中反馈电流的任何变化都必须是由离子电流 $i_{ion}$ 引起的，因此可测出该电流值。将细胞膜超极化到一个很低的电压值， $I_{Na},I_K$ 均可视为0，剩下的电流变化都是由泄露通道引起的，可通过拟合求出泄露电流的电导 $g_L$ 。

4.4 $I_{Na},I_K$ 的测量及其离子通道建模

Hodgkin和Huxley使用一种类似于 $Na^+$ 的带一份正电但不能透过细胞膜的有机离子胆碱消除 $Na^+$ 的内向电流，此时电压钳记录到 $K^+$ 的外向电流，之后可计算出 $Na^+$ 的电流。之后可计算出两个离子通道的电导。

根据当时已有的发现，Hodgkin和Huxley假设钠离子通道的数学形式为： $g_{Na}= \overline{g}_{Na}m^3h$ ，其中 $\overline{g}_{Na}$ 表示钠离子通道最大电导值， $m^3h$ 表示钠离子有三个独立的激活门控和一个独立的失活门控，当所有门控都打开时，钠离子才能通过。

同理，钾离子通道的电导表达式为： $g_K= \overline{g}_K n^x$ ，即有x个独立部分，当每个部位都打开时钾离子才能通过。Hodgkin和Huxley设计了一系列实验求出了x=4。

4.5 HH模型的数学表达

HH模型是一个四变量方程，每个变量对应一个常微分方程，其中一个是关于膜电位V的方程，另外三个是关于离子通道门控变量m\h\n的方程，模型的数学表达式如下：

其中门控变量的转换速率表达式为：

$I_{ext}$ 表示外界输入的电流， $\phi$ 为温度因子，开关状态的转换速率与温度成指数关系（对温度很敏感），表达式为 $\phi=Q_{10}^{(T-T_{base})/10}$ ，其中 $Q_{10}$ 为升高10℃的速率比。

4.6 HH模型的brainpy编程实现

模拟乌贼的神经元，对于乌贼的巨轴突， $T_{base}$ =6.3℃， $Q_{10}$ =3， $g_L=0.3mS/cm^2$ ， $E_L=-54.4mV$ ，编写HH模型代码如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class HH(bp.dyn.NeuGroup):
    def __init__(self,size,ENa=50.,gNa=120.,EK=-77.,gK=36.,EL=-54.387,
                 gL=0.03,V_th=20.,C=1.0,T=6.3):
        #初始化
        super(HH,self).__init__(size=size)

        self.ENa = ENa
        self.EK = EK
        self.EL = EL
        self.gNa = gNa
        self.gK = gK
        self.gL = gL
        self.C = C
        self.V_th = V_th
        self.Q10 = 3.
        self.T_base = 6.3
        self.phi = self.Q10**((T-self.T_base)/10)
        #定义神经元变量
        self.V = bm.Variable(-70.68 * bm.ones(self.num)) #膜电位
        self.m = bm.Variable(0.0266 * bm.ones(self.num)) #离子通道m
        self.h = bm.Variable(0.772 * bm.ones(self.num)) #离子通道h
        self.n = bm.Variable(0.235 * bm.ones(self.num)) #离子通道n
        self.input = bm.Variable(bm.zeros(self.num)) #神经元接收到的输入电流
        self.spike = bm.Variable(bm.zeros(self.num,dtype=bool)) #神经元发放状态
        self.t_last_spike = bm.Variable(bm.ones(self.num) * -1e7) 
        #神经元上次发放的时刻

        #积分函数定义
        self.integral = bp.odeint(f=self.derivative,method='exp_auto')

    @property
    def derivative(self):
        return bp.JointEq(self.dV,self.dm,self.dh,self.dn)

    #微分方程的定义
    def dm(self, m, t,V):
        alpha = 0.1 * (V + 40) / (1 - bm.exp(-(V + 40) / 10))
        beta = 4.0 * bm.exp(-(V + 65) / 18)
        dmdt = alpha * (1 - m) - beta * m
        return self.phi * dmdt

    def dh(self, h, t, V):
        alpha = 0.07 * bm.exp(-(V + 65) / 20.)
        beta = 1 / (1 + bm.exp(-(V + 35) / 10))
        dhdt = alpha * (1 - h) - beta * h
        return self.phi * dhdt

    def dn(self, n, t, V):
        alpha = 0.01 * (V + 55) / (1 - bm.exp(-(V + 55) / 10))
        beta = 0.125 * bm.exp(-(V + 65) / 80)
        dndt = alpha * (1 - n) - beta * n
        return self.phi * dndt

    def dV(self, V, t, m, h, n):
        I_Na = (self.gNa * m ** 3.0 * h) * (V - self.ENa)
        I_K = (self.gK * n ** 4.0) * (V - self.EK)
        I_leak = self.gL * (V - self.EL)
        dVdt = (- I_Na - I_K - I_leak + self.input) / self.C
        return dVdt

    #更新函数:每个事件步都运行此函数，完成变量更新
    def update(self,tdi):
        t,dt = tdi.t,tdi.dt
        #更新下一时刻变量值
        V,m,h,n = self.integral(self.V,self.m,self.h,self.n,t,dt=dt)
        #判断神经元是否产生动作电位
        self.spike.value = bm.logical_and(self.V < self.V_th, V >= self.V_th)
        #更新神经元发放的时间
        self.t_last_spike.value = bm.where(self.spike,t,self.t_last_spike)
        self.V.value = V
        self.m.value = m
        self.n.value = n
        self.h.value = h
        self.input[:]=0. #重置神经元接收到的输入

实验1：探究HH模型对不同大小外界输入的响应

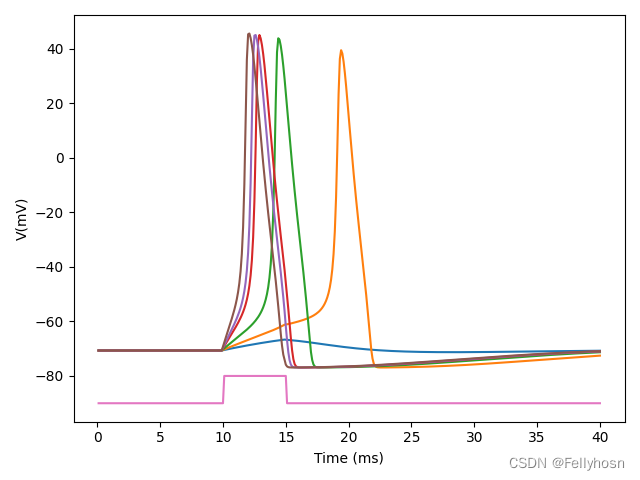
使用brainpy.inputs.section_input()函数来设置时长5毫秒的不同大小的外界输入，设置第一个时段长 10 毫秒，电流大小为 0；第二个时段长 5毫秒，每个神经元接收到的电流输入大小各不相同；第三个时段长 25 毫秒，电流大小再次被置为 0，建立一个brainpy.DSRunner来运行模型。

#探究HH模型对不同大小的外界输入的响应
currents,length = bp.inputs.section_input(
    values=[0.,bm.asarray([1.,2.,4.,8.,10.,15.]),0.],#分别接受电流大小为1/2/4/8/10/15
    durations=[10,5,25], #第一个时间段10ms 电流为0 第二个时间段5ms 接受不同大小的电流输入
    return_length=True)  #  第三个时间段25ms 电流再次为0
#建立brainpy.DSRunner来运行模型
hh = HH(currents.shape[1])
runner = bp.dyn.DSRunner(hh,monitors=['V','m','h','n'],inputs=['input',currents,'iter'])
runner.run(length)
#可视化
bp.visualize.line_plot(runner.mon.ts,runner.mon.V,ylabel='V(mV)',
                       plot_ids=np.arange(currents.shape[1]),)
plt.plot(runner.mon.ts,bm.where(currents[:,-1]>0,10.,0.).numpy() -90)
plt.tight_layout()
plt.show()

可以看出，HH模型存在全或无特征：当施加的电流低于某一阈值时，膜电位迅速恢复到静息状态；当电流超过某个阈值时，就会产生动作电位。

实验2：探究HH模型对持续电流的周期性响应

设置电流输入时间为50ms

#探究对持续时长输入的相应
currents,length = bp.inputs.section_input(values=[0.,10.,0.],
                                          durations=[10,50,10],
                                          return_length=True)
hh=HH(1)
runner = bp.dyn.DSRunner(hh,monitors=['V','m','h','n'],
                         inputs=['input',currents,'iter'])
runner.run(length)
bp.visualize.line_plot(runner.mon.ts,runner.mon.V,ylabel='V(mV)')
plt.plot(runner.mon.ts,bm.where(currents>0,10.,0.).numpy() -90)
plt.tight_layout()
plt.show()

当输入电流足够大并保持足够长的时间时，模型将产生周期性响应。

华为开发者联盟HarmonyOS专区

鸿蒙生态一站式服务平台。

更多推荐

Xenomai (学习笔记)

文章目录1. 简介1.1 实时OS1.2 Adeos域 (Domain)中断管道（Interrupt Pipe）事件管道(event pipeline)乐观的中断保护系统事件传播基于Linux的实现1.3 Adeos为Xenomai提供的服务Xenomai的主要和次要域名系统调用拦截中断传播启用/禁用中断源在域之间共享中断中断共享和延迟结论Xenomai用户层实时的实现(TSC)Xenomai多A